Lanzhou University is studying master's degree, focusing on unmanned driving and deep learning; the backbone of the unmanned vehicle team of Landa Future Computing Institute is changing its own unmanned vehicle, and has participated in many unmanned car Hackathon, and likes Extreme Programming.
In the first few decades, neural networks did not receive much attention. Until the emergence of deep learning, people used deep learning to solve a lot of practical problems (that is, some commercial applications that fall to the ground). The neural network has become a concern in the academic and industrial fields. One of the focal points. This paper presents three typical neural networks in deep learning and a regularization approach in deep learning in a straightforward and simple way as possible. For the future in the driverless application.

能力Intensive learning ability
There are many recent criticisms of deep learning in the academic field (see Gary Marcus's article: https://arxiv.org/ftp/arxiv/papers/1801/1801.00631.pdf). Deep learning is not seen by some scholars. The road to universal artificial intelligence. However, as researchers and engineers focusing on industrial applications, we do not need to pay attention to whether deep learning is the path to the ultimate universal artificial intelligence. We only need to know that deep learning cannot solve some problems in our industry. Problems that are difficult to solve through traditional software engineering)? The answer is yes. It is precisely because deep learning has such a capability. It has become the first technology in the history of artificial intelligence research for major commercial companies. (The artificial intelligence in the past was mostly a laboratory product and never attracted giants. A lot of capital investment). Business companies are pursuing interests and chasing commercialization. A technology can be used by a large number of companies in the industry to demonstrate that they already have the ability to commercialize and commercialize certain application industries. Let's first look at what deep learning now has. Product Force":
Image recognition and classification
Traditional computer vision techniques often require human design features when dealing with image recognition problems. To identify different categories, we must design different characteristics. To identify cats and dogs, we must design features for cats and dogs respectively. This process is Very troublesome, we use cats and dogs as examples:

The picture above is a picture of a cat and a dog. It can be said that it takes a lot of energy to design the features for both cat and dog recognition, and it must be a “dog and cat expert†to do this. So when the category to be identified rises to 1000? The recognition accuracy of traditional visual algorithms will be lower.
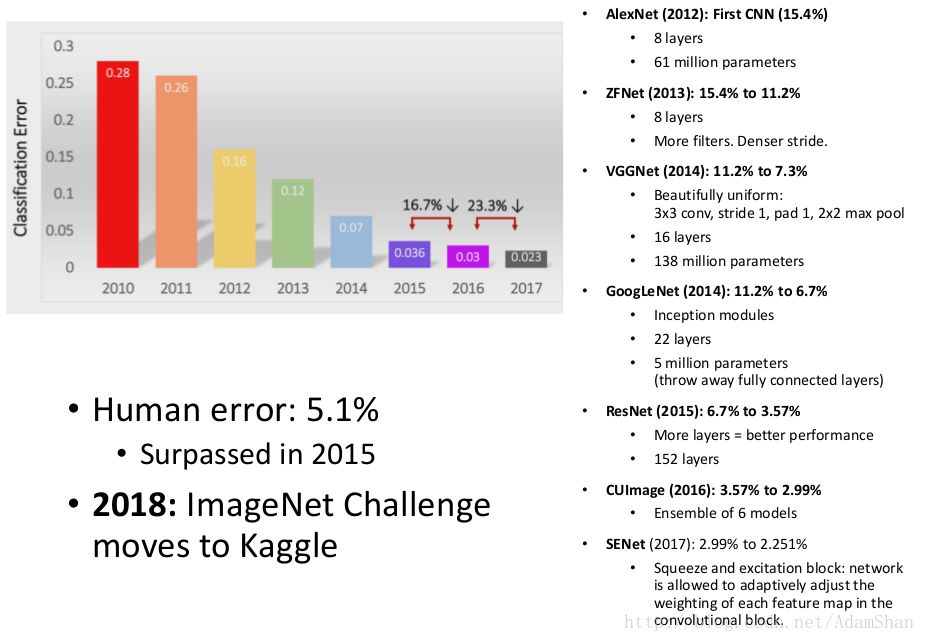
The first major breakthrough in deep learning was at ImageNet's recognition challenge.
ImageNet is a huge data set with 14 million images. Based on the ImageNet data set, the ILSVRC (ImageNet Large Scale Visual Recognition Challenge) Challenge is held once a year.
Since AlexNet broke the record of the year with ILSVRC's recognition rate far beyond the second in 2012, the recognition rate of deep learning on the ImageNet data set has achieved breakthroughs in the past two years. By 2015, ResNet's top-5 recognition rate officially exceeded humans:
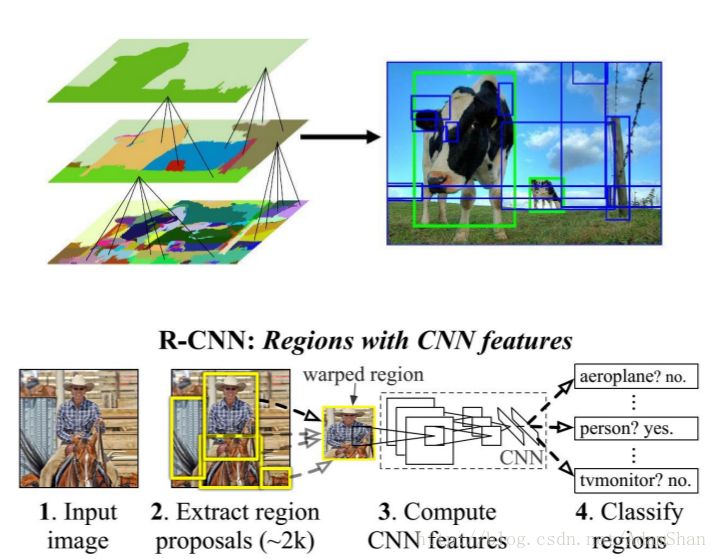
Target Detection
Pixel level scene segmentation

Video caption generation

Games and Chess

Speech recognition, text generation, automatic coloring of black and white films, Yalta games...
Deep learning has a strong ability to express complex tasks that can be handled. Naturally, we need to use deep learning to solve the long-standing problems of unmanned driving (computer vision based on deep learning, decision-making based on deep learning, reinforcement-based learning Decisions, etc.). Here we begin the relevant foundation of deep learning.
▌ Deep feedforward neural network - why deep?
At the end of the ninth blog, we actually had contact with a deep feed forward neural network. We used a very large depth feed forward network to solve the MNIST handwriting recognition problem. Our network achieved 98% 98% recognition rate. . In simple terms, the deep feed forward network is the “enhanced version†of the earlier three-tier BP network, as shown in the figure:
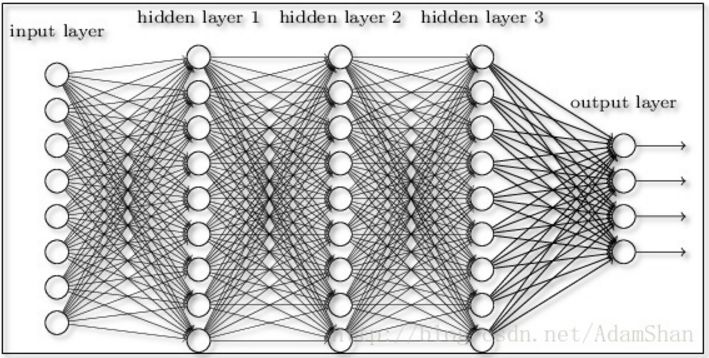
The layers are what we call full connection layers. So according to the introduction of the previous neural network, we know that even if we only use a 3-layer neural network, we can fit an arbitrary function. The neural network often follows the Occam's razor principle when designing, that is, we often use the simplest Structural modeling, then why should we deepen the number of network layers?
This problem needs to be viewed in two aspects: First, the efficiency of model training under big data, and one means learning.
The efficiency of model training under big data
Some people attributed the causes of deep learning breakthroughs to three factors:
Neural network theory (theoretical basis)
Large amount of data (thanks to the development of the Internet)
Greater contemporary parallel computing capabilities (represented by GPU computing)
The large amount of data is an important factor for deep neural networks to be successful in performance. Traditional machine learning algorithms seem to fall into a performance bottleneck after the data volume increases to a certain order of magnitude (even if based on structural risk minimization support. A vector machine whose performance will also saturate after a certain amount of data has reached a certain level, but the neural network seems to be a machine learning algorithm that can be continuously expanded. The larger the amount of data, the higher the number of neurons and the layers of the hidden layers. Numbers, training more powerful neural networks, the change trend is roughly as follows:
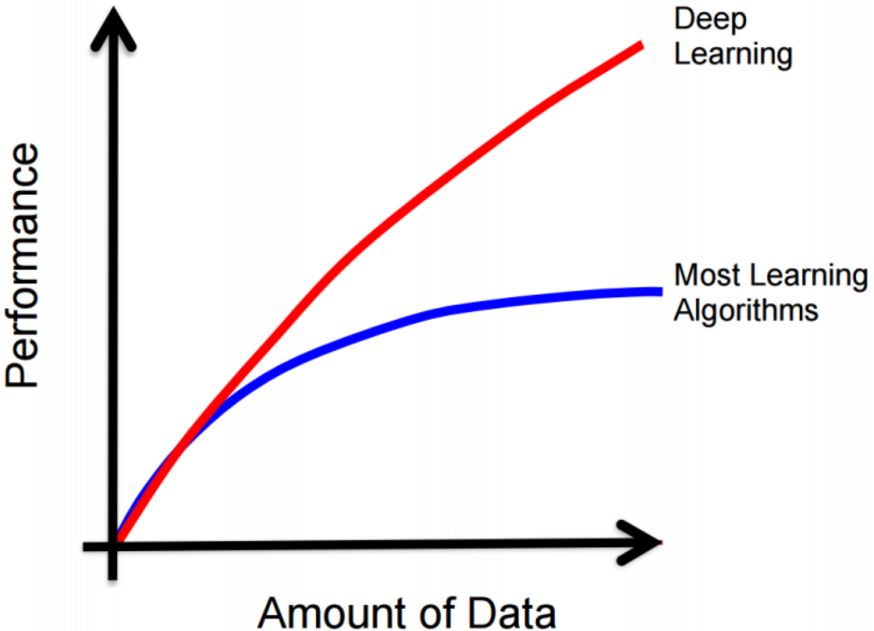
However, our previous article also mentioned that it can already be proved that only a simple three-layer neural network can theoretically fit any function by increasing the number of hidden layer neurons. So why don't we simply use a simple three-tier network structure and increase the number of hidden layer neurons to increase the model capacity so that we can fit complicated problems?
The model that can increase the number of single-layer neurons can have a stronger expression ability. However, compared to increasing the number of layers, each layer uses a relatively small number of neurons. The former is more difficult to train in actual training. The overfitting problem of three-layer networks containing a large number of hidden layer neurons is difficult to control, and to achieve the same performance, the structure of deep neural networks is often less than that of three-layer networks.
Express learning
Another explanation for the role of several layers before deep learning is to express learning. Depth learning = depth representation learning (characteristic learning). The following figure shows the visualization result of neural network hidden layer neuron activation after a multi-layer convolution network enters an image:
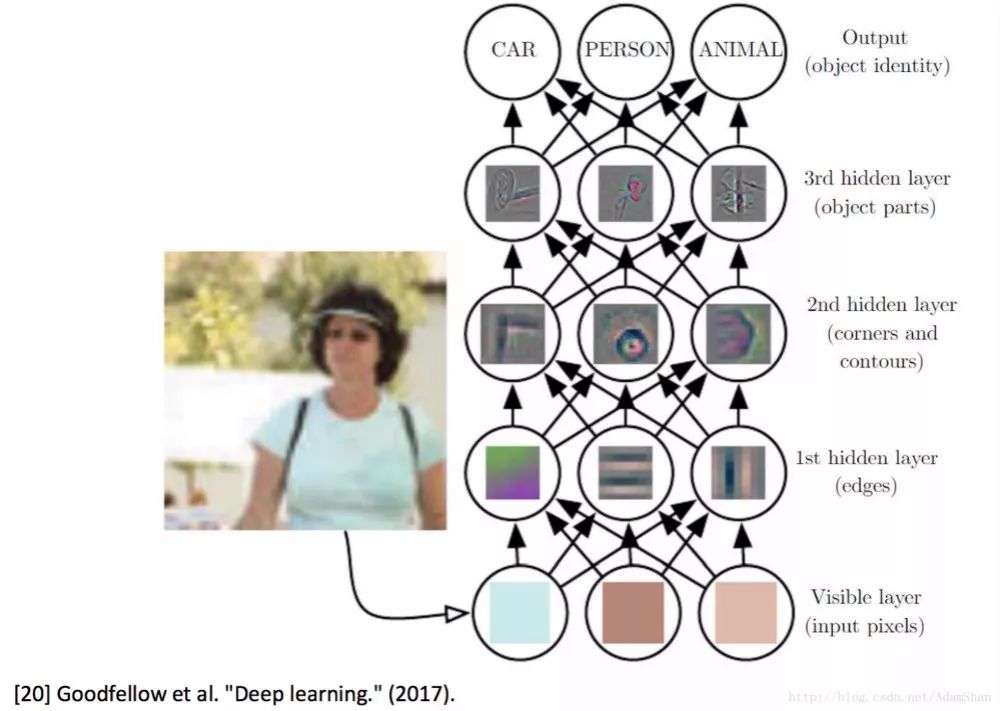
As shown in the figure, the first few layers of the neural network actually play this feature extraction and expression building role, distinguishing from the artificial design features of traditional machine learning methods, and the feature design of the neural network is accompanied by the training of the neural network. Automatically indicates the establishment process. From the figure we can also find out that the features that are closer to the input layer (the lower layer) are more simple to extract, and the higher the number of layers, the more complex the features created. For example, in the figure, the first layer extracts the "edge" feature, the second layer extracts the outline feature, and then the third hidden layer, through the combination of simple underlying features, synthesizes a more advanced representation, extracted It is a local feature that identifies the target. Through the layer-by-layer abstraction of features, the more layers of a neural network, the richer the feature representation it can build.
æ£Regularization techniques applied to deep neural networks
When the number of hidden layers and number of neurons in a neural network increases, the number of parameters increases substantially. This is because our neural network is easier to overfit, that is, the model performs well on the training set but has poor generalization ability. In machine learning, many strategies are explicitly designed to reduce test errors (which may be at the expense of increasing training errors). These strategies are collectively referred to as regularization.
Below we introduce four common regularization techniques. They are:
Data Agumentation
Early Stopping
Parameter Norm Penalties
Dropout
Dataset enhancements
One of the most intuitive strategies to enhance the robustness of machine learning is to use more data to train the model, ie dataset enhancement. However, in reality, our data is limited, so we often increase our data collection by creating fake data. For some machine learning tasks (such as image classification), creating fake data is very simple. , Here we use MNIST handwriting as an example to illustrate:
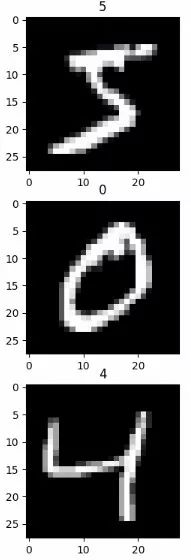
The three characters in the above figure are the three numbers in the training set of the MNIST data set. For such high-dimensional images and huge variability data, we can generate simple translation, rotation, scaling, etc. for the data. New data.
Def expend_training_data(train_x, train_y): """ Augment training data """ expanded_images = np.zeros([train_x.shape[0] * 5, train_x.shape[1], train_x.shape[2]]) expanded_labels = Np.zeros([train_x.shape[0] * 5]) counter = 0 for x, y in zip(train_x, train_y): # register original data expanded_images[counter, :, :] = x expanded_labels[counter] = y Counter = counter + 1 # get a value for the background # zero is the expected value, but median() is used to estimate background's value bg_value = np.median(x) # this is dictated as background's value for i in range (4 ): # rotate the image with random degree angle = np.random.randint(-15, 15, 1) new_img = ndimage.rotate(x, angle, reshape=False, cval=bg_value) # shift the image with random distance shift = np.random.randint(-2, 2, 2) new_img_ = ndimage.shift(new_img, shift, cval=bg_value) # register new training data expanded_images[counter, :, :] = ne W_img_ expanded_labels[counter] = y counter = counter + 1 return expanded_images, expanded_labelsagument_x, agument_y = expend_training_data(x_train[:3], y_train[:3])
Get a new data set that is 5 times the original data set:

The following four images are obtained through a certain transformation. We did not collect new data. By creating spurious data, our data set became several times the original. This processing method can significantly improve the neural network. Generalization ability, even if it is a translation-invariant convolutional neural network (which we will describe later), new data obtained using this simple processing method can also greatly improve generalization.
Early termination
When training neural networks with a large number of parameters, ie when the model capacity is greater than the actual demand, the neural network will always overfit, but we can always observe that the training error will gradually decrease with the training time, but verification The error of the set will decrease first and then increase, as shown in the following figure:
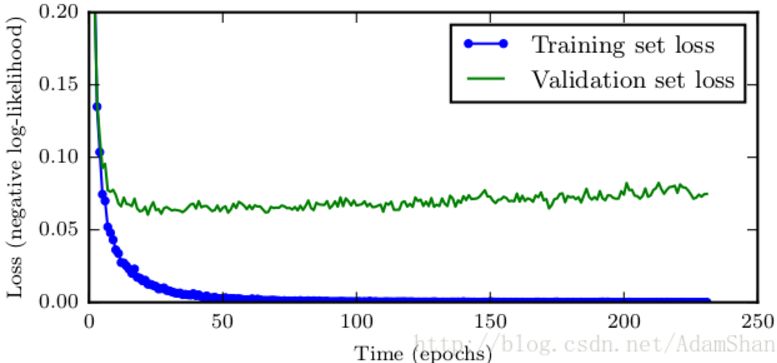
Based on this phenomenon, we can save a copy of the model after each observation that the error in the verification set has improved. If the error deteriorates, the patient value is +1. When the patient value reaches a preset threshold, Terminate training and return the last saved copy. In this way, we can get the model of the lowest point in the entire error curve.
Parametric norm punishment
Many regularization methods add a penalty term Ω(w) to the loss function L(θ) of the neural network to constrain the learning ability of the model once, in the following form:
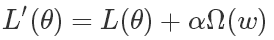
Where θ is a parameter of the neural network including weights and offsets (w, b). It should be noted that the penalty term often punishes only the weight (ie, w) in the affine transformation, and the bias unit b does not It is regularized because each weight clearly shows how the two variables interact. To fit the weights well, you need to observe these variables under a variety of different conditions. Each offset only controls a single variable, which means that there is no need to introduce too many variances while retaining the bias that is not regularized. Similarly, regularizing bias parameters introduces a considerable degree of under-fitting. Therefore, we often punish only the weight. α is a hyperparameter that needs to be set artificially. It is called the penalty coefficient. When α is 0, it means there is no parameter penalty. The larger α is, the larger the penalty of the corresponding parameter is. Let's take L2 regularization as an example. We added a regular term after the loss function:
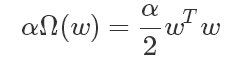
What is the result of minimizing the square of the weight?
Neural networks will tend to make all weights small unless the error derivative is too large.
Prevents fitting of wrong samples.
Making the model more "smooth" means that input and output sensitivity is lower, and small changes in the input will not be significantly reflected on the output.
If two identical inputs are entered at the input, the network's weight distribution will tend to divide the weights rather than assigning all the weights to one connection.
L2 punishment on the one hand reduces the degree of freedom of weighted learning and weakens the learning ability of the network. On the other hand, a relatively uniform weight makes the model smoother, making the model insensitive to subtle changes in the input, thus enhancing the robustness of the model. .
Dropout
The parametric norm penalizes the regularization by changing the loss function of the neural network, and Dropout enhances the generalization ability of the network by changing the structure of the neural network. The figure is a neural network training structure:
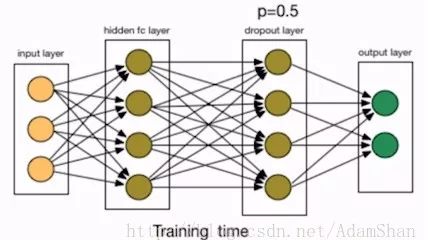
We added a Dropout layer behind the first hidden layer. Dropout refers to randomly deleting a node in the network, including the input and output edges of the node, as shown in the following figure:
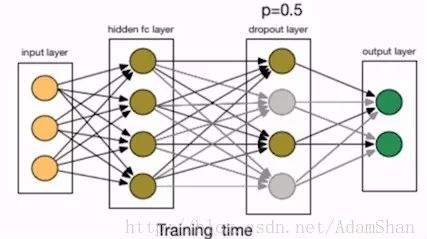
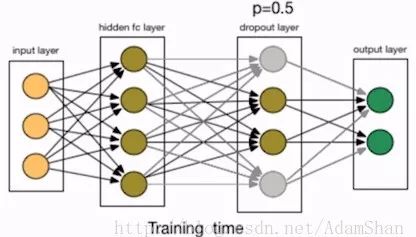
This is also equivalent to retaining nodes with a certain probability. In this example, p is the probability of retaining the node, we set it to 50%. In practice, the probability of retention is usually set at [0.5, 1]. So why does Dropout help prevent overfitting? The simple explanation is that the training process using dropout is equivalent to training a large number of neural networks with only half hidden units (hereinafter referred to as “half networkâ€). Each such half network can give a classification result. Some of these results are correct and some are wrong. As training progresses, most of the networks can give correct classification results, so a small number of misclassification results will not have a big impact on the final result.
Then when the training is over, our network can be regarded as an integrated model of many half networks. At the stage of application network, we will not use Dropout, that is, p=1. The final output of the network is all half. As a result of network integration, its generalization ability will naturally be better.
交通Traffic Signal Recognition Based on Deep Feedforward Neural Network
Belgium Traffic Sign Dataset Dataset
We use the Belgium TS (Belgium Traffic Sign Dataset) as a simple identification example. The BelgiumTS is a traffic signal data set containing 62 traffic signals.
Download link for training set:
http://btsd.ethz.ch/shareddata/BelgiumTSC/BelgiumTSC_Training.zip
Download link for test set: http://btsd.ethz.ch/shareddata/BelgiumTSC/BelgiumTSC_Testing.zip
This dataset is slow to download when not using scientific Internet access.
Reading and Visualizing Data
After downloading the data, unzip it and use the following directory structure to store the data:
Data/Training/data/Testing/
The data set's training set and test set both contained 62 directories representing 62 traffic signals. Use the following function to read the data:
Def load_data(data_dir): """Loads a data set and returns two lists: images: a list of Numpy arrays, each representing an image. labels: a list of numbers that represent the images labels. """ # Get all subdirectories Of data_dir. Each represents a label. directories = [d for d in os.listdir(data_dir) if os.path.isdir(os.path.join(data_dir, d))] # Loop through the label directories and collect the data In # two lists, labels and images. labels = [] images = [] for d in directories: label_dir = os.path.join(data_dir, d) file_names = [os.path.join(label_dir, f) for f in Os.listdir(label_dir) if f.endswith(".ppm")] # For each label, load it's images and add them to the images list. # And add the label number (ie directory name) to the labels list. f in file_names: images.append(skimage.data.imread(f)) labels.append(int(d)) return images, labels # Load training and testing datasets.ROOT_PATH = "data"train_dat A_dir = os.path.join(ROOT_PATH, "Training")test_data_dir = os.path.join(ROOT_PATH, "Testing")images, labels = load_data(train_data_dir)
Output the number of classes and the total number of pictures in the training set:
Print("Unique Labels: {0}Total Images: {1}".format(len(set(labels)), len(images)))
Unique Labels: 62Total Images: 4575
We show the first picture of each category to see.
Def display_images_and_labels(images, labels): """Display the first image of each label.""" unique_labels = set(labels) plt.figure(figsize=(15, 15)) i = 1 for label in unique_labels: # Pick The first image for each label. image = images[labels.index(label)] plt.subplot(8, 8, i) # A grid of 8 rows x 8 columns plt.axis('off') plt.title(" Label {0} ({1})".format(label, labels.count(label))) i += 1 _ = plt.imshow(image) plt.show()display_images_and_labels(images, labels)

Obviously, the images of the dataset are not uniform in size. To train the neural network, we need to resize all the images to the same size. In this article, we resize the images to (32,32):
# Resize imagesimages32 = [skimage.transform.resize(image, (32, 32)) for image in images]display_images_and_labels(images32, labels)

Output image information after resize:
For image in images32[:5]: print("shape: {0}, min: {1}, max: {2}".format(image.shape, image.min(), image.max()))
Shape: (32, 32, 3), min: 0.0, max: 1.0shape: (32, 32, 3), min: 0.13088235294117614, max: 1.0shape: (32, 32, 3), min: 0.057059972426470276, max: 0.9011967677696078shape: (32, 32, 3), min: 0.023820465686273988, max: 1.0shape: (32, 32, 3), min: 0.023690257352941196, max: 1.0
The range of values ​​of the image has been normalized. Next we use TensorFlow to construct a neural network to train a deep feedforward network to identify this traffic signal.
Data preprocessing
We preprocess the data by first converting the three channels of RGB to grayscale:
Images_a = color.rgb2gray(images_a)display_images_and_labels(images_a, labels)

Note that this is not a grayscale image, because we used the previous display_images_and_labels function. We only need to add cmap='gray' to the imshow part of the function to display the grayscale image.
We use the previous method to expand the data (expand the data to 5 times the original), and we actually show three of them:

We then shuffle the data and divide the data into training and validation sets and perform one-hot encoding of the tags:
From sklearn.utils import shuffleindx = np.arange(0, len(labels_a)) indx = shuffle(indx)images_a = images_a[indx]labels_a = labels_a[indx]print(images_a.shape, labels_a.shape)train_x, val_x = Images_a[:20000], images_a[20000:]train_y, val_y = labels_a[:20000], labels_a[20000:]train_y = keras.utils.to_categorical(train_y, 62)val_y = keras.utils.to_categorical(val_y, 62) Print(train_x.shape, train_y.shape)
▌ Use Keras to construct and train deep feedforward networks
We still use the deep feed forward network we used in the previous article to see how performance is in such complex problems:
Model = Sequential() model.add(Flatten(input_shape=(32, 32))) model.add(Dense(512, activation='relu')) model.add(Dropout(0.5)) model.add(Dense( 512, activation='relu')) model.add(Dropout(0.5)) model.add(Dense(62, activation='softmax')) model.summary()model.compile(loss='categorical_crossentropy', optimizer= RMSprop(), metrics=['accuracy']) history = model.fit(train_x, train_y, batch_size=128, epochs=20, verbose=1, validation_data=(val_x, val_y)) ### print the keys contained in The history objectprint(history.history.keys())model.save('model.json')
Real-life training loss and verification loss for:
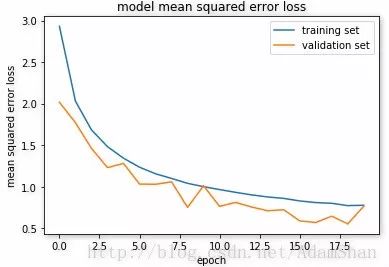
Load the test data set to see the accuracy:
('Test loss:', 0.8060373229994661)('Test accuracy:', 0.7932539684431893)
Our simple neural network achieved a 79% accuracy on the test set. We realistically predicted the results of several test samples:

Although the accuracy is not high, the effect seems to be fine. . Of course, this example is just an introductory network. First, it discards the 3-channel image, so there will be some loss of information. Second, the first step in fully connected networks is to vectorize the image. Can we use it more deeply? , more in line with the two-dimensional features of the picture network? We continue to explore in the next article!
Complete code link:
Http://download.csdn.net/download/adamshan/10217607
Original link:
Https://blog.csdn.net/adamshan/article/details/79127573
Ningbo Autrends International Trade Co.,Ltd. , https://www.ecigarettevapepods.com