In this article, we will discuss the commonly used non-comparative sorting algorithms: counting sorting, cardinality sorting, bucket sorting. Under certain conditions, their time complexity can reach O (n).
The only data structure we use here is an array. Of course, we can also use a linked list to implement the following algorithm.
Counting Sort (Counting Sort)
Count sorting uses an additional count array C, according to the array C to arrange the elements of the original array A to the correct position.
It is generally understood that, for example, there are 10 people of different ages. If eight people are counted as being no older than Xiaoming (that is, less than or equal to Xiaoming ’s age, including Xiaoming), then Xiaoming ’s age is ranked 8th. Through this kind of thinking, everyone's position can be determined, and the order is arranged. Of course, special treatment is needed when the age is the same (to ensure stability): by reversely filling the target array, the corresponding number statistics will be decremented after filling, which can ensure the stability of the counting order.
The steps of counting and sorting are as follows:
Count the number of occurrences of each value A [i] in the array A, and store it in C [A [i]]
From front to back, make each value in array C equal to its addition to the previous item, so that array C [A [i]] becomes the number of elements in array A that is less than or equal to A [i]
Backfill the target array B: place the array element A [i] at the C [A [i]] position of the array B (the subscript is C [A [i]] – 1). C [A [i]] decreasing
The implementation code of counting sort is as follows:
#include
using namespacestd;
// Classification ------------ Internal non-comparison sort
// Data structure --------- array
// Worst time complexity-O (n + k)
// Optimal time complexity-O (n + k)
// Average time complexity-O (n + k)
// Auxiliary space required ------ O (n + k)
// Stability --------- Stability
constintk = 100; // cardinality is 100, sort integers in [0,99]
intC [k]; // count array
voidCountingSort (intA [], intn)
{
for (inti = 0; i
{
C [i] = 0;
}
for (inti = 0; i
{
C [A [i]] ++;
}
for (inti = 1; i
{
C [i] = C [i] + C [i-1];
}
int * B = (int *) malloc ((n) * sizeof (int)); // Allocation of temporary space, length n, used to temporarily store intermediate data
for (inti = n-1; i> = 0; i--) // Scan from back to front to ensure the stability of the counting order (the relative order of repeated elements is unchanged)
{
B [-C [A [i]]] = A [i]; // Put each element A [i] in its correct position in the output array B
// When the repeated element is encountered again, it will be placed in the previous position of the current element to ensure the stability of the counting order
}
for (inti = 0; i
{
A [i] = B [i];
}
free (B); // Free temporary space
}
intmain ()
{
intA [] = {15,22,19,46,27,73,1,19,8}; // The input designed for count sorting, each element is on [0,100] and has duplicate elements
intn = sizeof (A) / sizeof (int);
CountingSort (A, n);
printf ("Count and sort results:");
for (inti = 0; i
{
printf ("% d", A [i]);
}
printf ("");
return0;
}
The following figure shows a simple demonstration process of counting and sorting {4, 1, 3, 4, 3}
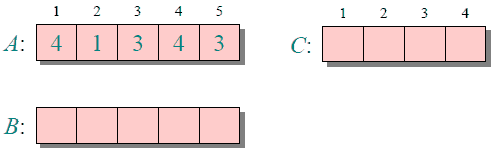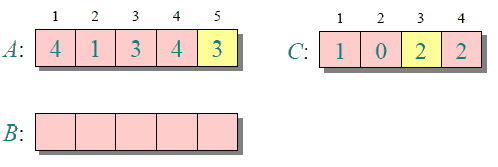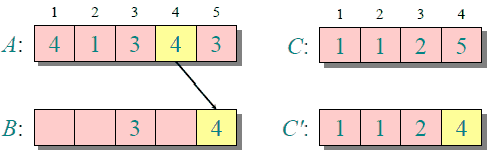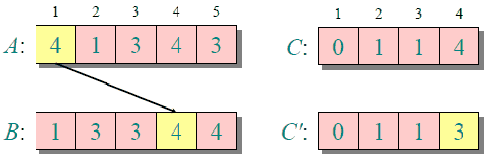
The time and space complexity of counting and sorting are related to the data range of array A (the difference between the maximum and minimum values ​​of elements in A plus 1), so for arrays with a large data range, counting and sorting requires a lot of time and memory .
For example: Sort numbers between 0 and 99. Counting sorting is the best algorithm. However, counting sorting is not suitable for sorting names in alphabetical order. Using counting sorting in cardinality sorting algorithm can sort the data range more effectively. Very large array.
Radix Sort
The invention of cardinality sorting can be traced back to the contribution of Hermann Holleri in 1887 on the punch card making machine. It is implemented in this way: all positive integers to be compared are unified to the same digit length, and numbers with shorter digits are preceded by zeros. Then, from the lowest bit to the base 10 count sorting, until the highest bit count sorting is completed, the sequence becomes an ordered sequence (using the stability of count sorting).
The implementation code of cardinality sorting is as follows:
#include
using namespacestd;
// Classification ------------- Internal non-comparison sort
// data structure -------- array
// Worst time complexity ---- O (n * dn)
// Optimal time complexity ---- O (n * dn)
// Average time complexity ---- O (n * dn)
// Auxiliary space needed ------ O (n * dn)
// Stability --------- Stability
constintdn = 3; // The elements to be sorted are three digits or less
constintk = 10; // The radix is ​​10, each digit is an integer in [0,9]
intC [k];
intGetDigit (intx, intd) // Get the d-th digit of element x
{
intradix [] = {1,1,10,100}; // The maximum number is three digits, so as long as the hundred digits are satisfied here
return (x / radix [d])% 10;
}
voidCountingSort (intA [], intn, intd) // Count and sort the A array according to the d-th digit of the element
{
for (inti = 0; i
{
C [i] = 0;
}
for (inti = 0; i
{
C [GetDigit (A [i], d)] ++;
}
for (inti = 1; i
{
C [i] = C [i] + C [i-1];
}
int * B = (int *) malloc (n * sizeof (int));
for (inti = n-1; i> = 0; i--)
{
intdight = GetDigit (A [i], d); // The current digit of element A [i] is right
B [-C [dight]] = A [i]; // According to the current digit, put each element A [i] in its correct position in the output array B
// When encountering an element whose current digit is the same as right, it will be placed in the previous position of the current element to ensure the stability of the counting order
}
for (inti = 0; i
{
A [i] = B [i];
}
free (B);
}
voidLsdRadixSort (intA [], intn) // lowest order first radix sort
{
for (intd = 1; d
CountingSort (A, n, d); // Count and sort A according to the d-th digit
}
intmain ()
{
intA [] = {20,90,64,289,998,365,852,123,789,456}; // The input designed for cardinality sorting
intn = sizeof (A) / sizeof (int);
LsdRadixSort (A, n);
printf ("Base Sorting Results:");
for (inti = 0; i
{
printf ("% d", A [i]);
}
printf ("");
return0;
}
The following figure shows a simple demonstration process of cardinal sorting on {329, 457, 657, 839, 436, 720, 355}
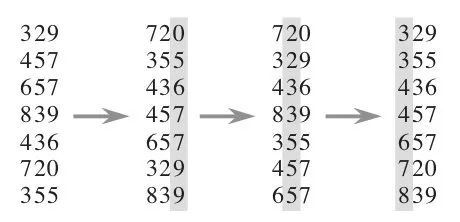
The time complexity of cardinality sorting is O (n * dn), where n is the number of elements to be sorted and dn is the number of digits. This time complexity is not necessarily better than O (n log n). The size of dn depends on the choice of digital bits (such as the number of bits) and the size of the complete set of data types to which the data to be sorted; dn determines how many rounds of processing , And n is the number of operations processed per round.
If the comparison with comparison sorting is considered, the formal complexity of cardinality sorting is not necessarily smaller, but the cost of its basic operation is less because of no comparison, and if the cardinality is properly selected, dn is generally not greater than log n, so Cardinality sorting is generally faster than comparison-based sorting, such as quick sorting. Since integers can also express strings (such as names or dates) and floating-point numbers in a specific format, radix sorting is not limited to integer sorting.
Bucket Sort
Bucket sorting is also called box sorting. The working principle is to map the array elements into a limited number of buckets, and use the counting sort to locate the boundaries of the buckets, and each bucket can be sorted within the bucket (using other sorting algorithms or recursively continue to use bucket sorting).
The implementation code for bucket sorting is as follows:
#include
using namespacestd;
// Classification ------------- Internal non-comparison sort
// Data structure --------- array
// Worst time complexity-O (nlogn) or O (n ^ 2), there is only one bucket, depending on the sorting method in the bucket
// Optimal time complexity ---- O (n), each element occupies one bucket
// Average time complexity ---- O (n), to ensure that the number of elements in each bucket is uniform
// Required auxiliary space ------ O (n + bn)
// Stability --------- Stability
/ * This program uses arrays to simulate buckets * /
constintbn = 5; // To sort the elements of [0,49], it is enough to use 5 buckets, and the number of buckets can also be determined dynamically based on the input
intC [bn]; // Count array to store the boundary information of the bucket
voidInsertionSort (intA [], intleft, intright)
{
for (inti = left + 1; i
{
intget = A [i];
intj = i-1;
while (j> = left && A [j]> get)
{
A [j + 1] = A [j];
j--;
}
A [j + 1] = get;
}
}
intMapToBucket (intx)
{
returnx / 10; // The mapping function f (x), which is equivalent to Partition in the quick queue, divides a large amount of data into basically ordered data blocks
}
voidCountingSort (intA [], intn)
{
for (inti = 0; i
{
C [i] = 0;
}
for (inti = 0; i
{
C [MapToBucket (A [i])] ++;
}
for (inti = 1; i
{
C [i] = C [i] + C [i-1];
}
int * B = (int *) malloc ((n) * sizeof (int));
for (inti = n-1; i> = 0; i--) // Scan from back to front to ensure the stability of the counting order (the relative order of repeated elements is unchanged)
{
intb = MapToBucket (A [i]); // element A [i] is in bucket b
B [-C [b]] = A [i]; // Put each element A [i] in its correct position in the output array B
// The boundary of the bucket is updated: C [b] is the position of the first element of bucket b
}
for (inti = 0; i
{
A [i] = B [i];
}
free (B);
}
voidBucketSort (intA [], intn)
{
CountingSort (A, n); // Use counting sort to determine the boundaries of each bucket
for (inti = 0; i
{
intleft = C [i]; // C [i] is the position of the first element in bucket i
intright = (i == bn-1? n-1: C [i + 1]-1); // C [i + 1] -1 is the position of the last element in bucket i
if (left
InsertionSort (A, left, right);
}
}
intmain ()
{
intA [] = {29,25,3,49,9,37,21,43}; // input designed for bucket sorting
intn = sizeof (A) / sizeof (int);
BucketSort (A, n);
printf ("bucket sorting result:");
for (inti = 0; i
{
printf ("% d", A [i]);
}
printf ("");
return0;
}
The following figure shows a simple demo process of bucket sorting on {29, 25, 3, 49, 9, 37, 21, 43}
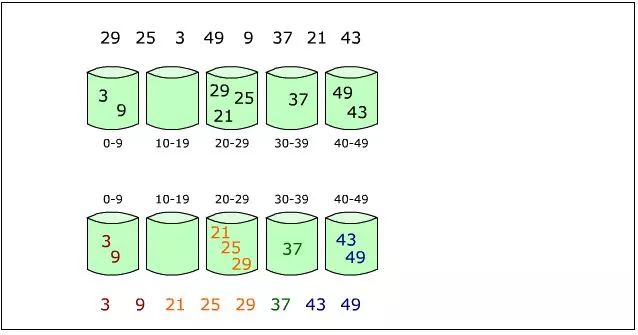
Bucket sorting is not a comparative sorting and is not affected by the lower limit of O (nlogn). It is an inductive result of pigeon nest sorting. When the array values ​​to be sorted are evenly distributed, bucket sorting has linear time complexity.
10-inch tablet devices have greatly surpassed netbooks in terms of entertainment, including reading, games, and audio-visual enjoyment. In other respects, the basic operation of the 10-inch tablet computer built on the touch screen ensures that the application of the tablet computer can be well realized, and its operation performance is closer to that of a smartphone.
1.In appearance, the 10-inches tablet computer looks like a large-screen mobile phone, or more like a separate LCD screen.
2.In terms of hardware configuration, the 10-inches tablet computer has all the hardware devices of a traditional computer, and has its own unique operating system, compatible with a variety of applications, and has a complete set of computer functions.
3.The 10-inches tablet computer is a miniaturized computer. Compared with traditional desktop computers, tablet computers are mobile and flexible. Compared with Laptops, tablets are smaller and more portable
4.The 10-inches tablet is a digital notebook with digital ink function. In daily use, you can use the tablet computer like an ordinary notebook, take notes anytime and anywhere, and leave your own notes in electronic texts and documents.
10 Inches Tablet Pc,Tablet Pc Android,10 Inch Quad Core Tablet,Tablet 10 Inch
Jingjiang Gisen Technology Co.,Ltd , https://www.jsgisentec.com