0 Preface
At present, the all-round mobile robot has become the most ideal choice for the RoboCup medium-sized soccer robot competition due to its excellent flexibility. The motion control of robots has always been a major factor directly affecting the performance of robots, and it is also one of the hotspots of mobile robot research. This paper studies a method of implementing three-wheel omnidirectional mobile robot motion control system by FPGA technology. Compared with dual DSP structure, DSP+CPLD structure, and DSP+ ASIC structure, this method is simple, reliable and extensible. Features. And the FPGA design is simple, easy to use, short development cycle, and can realize the real SOPC system.
1 Omnidirectional mobile robot motion model
Let the speed of the robot in the world coordinate system be ε=[vx, vy, φ], then when vx=O, vy≠0, φ=O, the robot will do the linear motion in the front-rear direction, when vx≠0, vy=0 When φ=0, the robot performs linear motion in the left and right direction. When vx=0, vy=0, φ≠0, the robot performs the rotation motion. In Fig. 1, ω1, ω2, ω3 are the rotational angular velocities of three driving wheels, R is the omnidirectional wheel radius; L1, L2, L3 are the horizontal distances from the center of the robot body to the center of the three sets of omnidirectional wheels, with L1= L2 = L3 = L. α is the angle between the first two rounds, and the other two angles are 180°-α/2. The relationship between the speed in the robot coordinate system and the three-wheel speed is as follows:
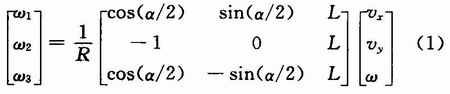
It can be seen from equation (1) that after knowing the speed requirement of the robot in the plane world coordinate system, the speed requirement of the driving wheel can be obtained, and then the corresponding control signal is sent to the motor.
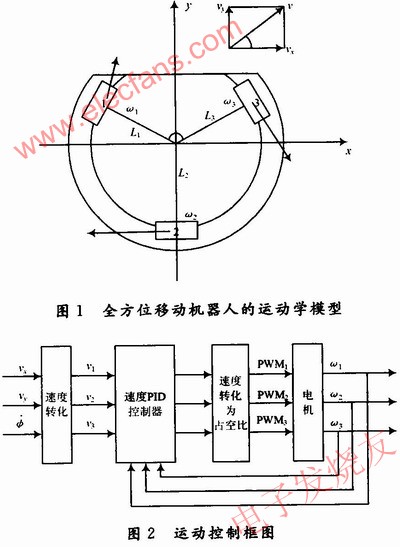
2 motion control scheme The overall design idea of ​​the system is shown in Figure 2. Firstly, the communication between the PC and the underlying control chip FPGA is realized through the RS 232 interface. After receiving the speed of the relevant robot coordinate system, the FPGA will connect the robot coordinate system. The lower speed value is converted into the angular velocity of the three omnidirectional wheels of the robot, and the obtained angular velocity value is calculated to the corresponding duty ratio to generate a PWM waveform of the corresponding duty ratio, and the output signal is connected to the DC servo motor driver, and then collected by the FPGA. Orthogonally encode the disc signal, calculate the actual angular velocity value of the wheel, and do the PID speed closed-loop control. In view of the advantages of FPGA module replication, PID closed-loop control is performed for each omnidirectional wheel.
3 system hardware design
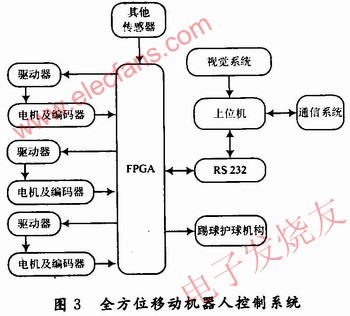
The block diagram of the three-wheel omnidirectional mobile robot system used is shown in Figure 3. The host computer mainly completes the image information acquisition, processing, path planning, and realizes communication with the off-site referee box. The lower computer is mainly FPGA, which mainly realizes the acquisition of three-round coded signals, PID speed closed-loop control, kick control, motor control signal generation, and other sensor information collection, etc., and is responsible for information interaction with the host computer. . This design only completes the motion control part of the lower computer.
3.1 Orthogonal coded signal acquisition and speed measurement
The incremental photoelectric encoder output signal is shown in Figure 4.
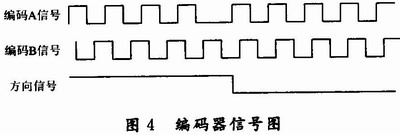
The A and B two-phase signals are orthogonal square wave pulse trains with phase differences of 90°. Each pulse represents a certain angle of rotation of the object to be measured, and the phase relationship between A and B reflects the rotation direction of the object to be measured. In the FPGA design 4 times the frequency and direction-correcting circuit, this design uses 2 outputs: one output direction, the other output pulse, and simulates the direction-doubling circuit, as shown in Figure 5.

There are three methods for measuring the rotational speed according to the pulse count, the M method, the T method, and the M/T method. The M method is suitable for high-speed measurement occasions, and has a large error at low speeds; while the T method, on the contrary, is accurate at low speeds and large at high speeds.
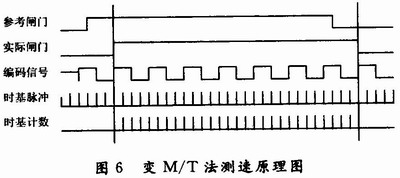
This design uses the method described in the literature. The method is as shown in FIG. 6, and the reference gate time is set to a fixed value, which is only used as a reference signal and an encoded signal to determine the actual gate time. The gate time thus determined is the whole cycle times of the signal to be measured, which can effectively improve the measurement accuracy. Then the measured speed is:
4. Incremental PID Control Principle and FPGA Implementation
The mathematical model of the actual robot inevitably has a certain degree of parameter uncertainty, and the orthogonal omnidirectional wheel of the three-wheel omnidirectional mobile robot will alternately contact the ground during walking to generate some uncertain friction torque, which will give The precise control of the robot brings difficulty. In order to accurately control the three-wheel omnidirectional mobile robot, the system uses the PID speed closed-loop control algorithm to adjust the speed of the three omnidirectional wheels of the robot.
Let the sampling period be TS, and discretize the continuous PID formula to get the digital PID algorithm expression:
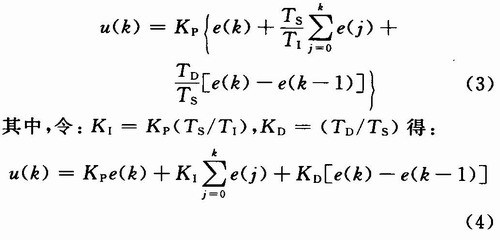
Where k is the sample number; u(k) is the computer output value at the kth sampling time; e(k) is the computer input error value at the kth sampling time; e(k-1) is the k-1th The input error value at the sampling time; Kp is the proportional coefficient; KI is the integral coefficient; KD is the differential coefficient.
Although this algorithm is relatively intuitive, since it is a full output, each output is related to all past states. When calculating, e(k) is accumulated and the amount of computer operations is large.
The incremental PID algorithm was generated:
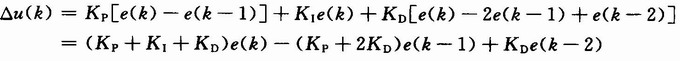
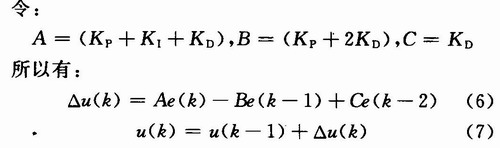
The above formula (7) is an incremental PID control algorithm. Only the control increment is output, the influence of the malfunction is small, and the control increment is only related to the sample values ​​of the last few times, and it is easy to obtain a better control effect by the weighting process.
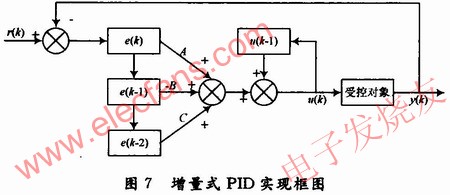
Based on the above formula, combined with the working characteristics of FPGA, this paper designs an incremental PID implementation structure suitable for FPGA.
It can be seen from Fig. 7 that the incremental PID control algorithm program structure can be weighted as long as the last three error sample values ​​are used. This can be completely implemented in parallel within the FPGA. The shifting part structure is similar to the implementation structure of the FIR filter. The difficulty is the skilled operation of the signed number in the FPGA design and ensuring that the accumulator cannot overflow.
An efficient hardware test method and system test method, which can acquire and display the real-time signal of the programmable system-on-a-chip (SOPC), which can be downloaded to the FPGA along with the design file to capture the internal nodes of the FPGA and the I/O The state of the foot is like using a real logic analyzer to simulate the design online without affecting the work of the hardware system. In order to verify whether the measured actual speed value of the omnidirectional wheel is accurate, the designed speed measuring module is simulated online. Set each omni wheel to rotate at a fixed speed, and compare the measured actual speed value with the set speed value, as shown in Figure 8.

In the embedded logic analyzer, the PID module was also tested online. Experimental conditions: Under no-load conditions, the speed of the motor is frequently changed. The embedded logic analyzer is used to observe the speed value and set value of the internal PID adjustment of the FPGA. Figure 9 shows the speed setting value of the first omnidirectional wheel. With feedback speed value.
The three-wheel omni-directional mobile robot is different from the two-wheel differential, and has great flexibility. Moreover, due to the different loads of the three omnidirectional wheels, the robot cannot get out of the precise straight line. One of the prerequisites for precise control of the robot is to allow it to go straight out of a straight line. In order to test the robot control performance, the following experiment was designed: the robot walks in four directions, forward, backward, left and right at a fixed speed. First observe the situation when the PID control algorithm is not added, and then observe the situation when adding the PID control algorithm. The results of the experiment are shown in Table 1.

Analysis: Since the load of the three omnidirectional wheels of the robot is different, that is, under the same duty cycle PWM, the actual speeds of the three wheels are not the same, which makes it impossible for the three-wheel speed to accurately synthesize the robot. Speed, which in turn affects the robot's control trajectory. According to the load of the No. 1 wheel and the No. 3 wheel of the robot shown in Figure 1, the load on the No. 2 wheel is large. When the PID controller is not added, the front and rear movements are approximately straight in a certain range, but the speed of the robot is not up. To the expected set speed, the left and right motion trajectory is a circle, and the set left and right movement speed of the robot also determines whether the robot rotates clockwise or counterclockwise. After adding the PID control algorithm, the speed of the wheel is corrected, and the robot can move back and forth at the expected set speed, especially the left and right motion is approximately a straight line within a certain range, and is no longer a circle. It can be seen that the PID closed-loop control algorithm significantly improves the control performance of the robot.
5 Conclusion
Aiming at the common scheme of implementing the underlying motion control system of soccer robot with DSP as the core, a method of implementing the bottom motion control system of three-wheel omnidirectional mobile soccer robot using FPGA is proposed. Through the application practice on the three-wheeled soccer robot, it is found that the scheme implemented by FPGA has good real-time performance and high precision, and because of the many characteristics of the FPGA itself, its scalability is strong, for example, Other sensors such as digital compass and other peripheral information sensors are configured through the serial port. At the same time, this design has important reference value and practical value for studying the realization scheme of multi-motor robot motion control system.
In addition, since the omnidirectional wheel has strong follow-up and easy slippage, the direction is easily affected when precise control is implemented, and the PID closed-loop control algorithm takes longer to respond, and the parameters require more time for debugging. In the study, we will study more precise control algorithms to achieve precise control of the robot.
Welcome to reprint, this article from the electronic enthusiast network (http://)Bull nose is a common connecting way of Conveyor Belt, which is named for its shape.
The joint mesh is made of Kevlar coated with Teflon dispersion, whose technical is similar to PTFE open Mesh Conveyor Belt.
Compared to PTFE fabric conveyor belt, bull nose is much more suitable for open mesh conveyor belt, and easy to install and to repairing. In addition, the price is more competitive than alligator joint. Besides, the conveyor belt with bull nose can apply in micro wave situation.

PTFE Conveyor Belts With Bullnose
Industrial Conveyor Belts,Conveyor Belt With Bullnose,Mesh Conveyor Belt With Bullnose,PTFE Conveyor Belts With Bullnose
TAIZHOU YAXING PLASTIC INDUSTRY CO., LTD , http://www.yaxingptfe.com